소프트웨어 렌더러 만들기 - 18 (SIMD를 사용한 역제곱근)

여기까지의 작업내용: https://github.com/hwi-middle/HimchanSoftwareRenderer/tree/3f2aed191fb0b405330daf334ce697cdc54cb65b

GitHub - hwi-middle/HimchanSoftwareRenderer: C++로 구현한 소프트웨어 렌더러입니다.

시즌 213908호 '오랜만입니다'

종강 직후 3개월 동안 아르바이트를 시작했다. 게임회사에서 성능 프로파일링을 담당했는데, 기본적인 툴 사용법만 익히면 반복 작업이라서 아르바이트를 구한 모양이었다. 이걸로 학원비를 벌었고... 그렇게 또 다시 렌더러는 잠시 방치되었다.

저 이제 SIMD 할 줄 알아요

그 동안 나는 POCU에서 어셈블리어 프로그래밍을 수강했다. 6502 어셈블리부터 시작해서 x86-16, IA-32, x87 FPU까지 진하게 맛보고 SIMD도 맛보았다. 하여, 원래 언리얼 엔진의 코드를 볼 때 무슨 말인지 전혀 감을 못잡았던 SIMD 부분도 읽히게 되었다.

SIMD를 어디에 적용해볼까, 생각해봤는데 예전에 이런 글을 남겼던게 생각났다.

후후... 나도 이제 SIMD를 몸에 익혔겠다, 역제곱근을 구하는 부분을 SIMD로 짜보도록 하자!

언리얼 엔진의 GetInvSqrt 함수 분석

FORCEINLINE float InvSqrt(float InValue)
{
    const __m128 One = _mm_set_ss(1.0f);
    const __m128 Y0 = _mm_set_ss(InValue);
    const __m128 X0 = _mm_sqrt_ss(Y0);
    const __m128 R0 = _mm_div_ss(One, X0);
    float temp;
    _mm_store_ss(&temp, R0);
    return temp;
}

SIMD를 인라인 어셈블리로만 사용해봤기 때문에 이런 형태는 처음본다. 하지만 더 들여다보자.

typedef union __declspec(intrin_type) __declspec(align(16)) __m128 {
     float               m128_f32[4];
     unsigned __int64    m128_u64[2];
     __int8              m128_i8[16];
     __int16             m128_i16[8];
     __int32             m128_i32[4];
     __int64             m128_i64[2];
     unsigned __int8     m128_u8[16];
     unsigned __int16    m128_u16[8];
     unsigned __int32    m128_u32[4];
 } __m128;

먼저 __m128이 무엇인고... 하니 그냥 공용체로 128비트를 맞춰놓은거다. SSE 레지스터가 128비트니까. 그리고 이건 에픽게임즈가 짠 코드가 아니라 인텔에서 제공하는 코드였다(주석에 나와있었음). 헤더 파일 이름은 xmmintrin.h인데, xmm은 SSE 레지스터 이름이고 intrin은 intrinsic을 의미하는 것 같다.

 

intrinsic이라는 단어는 '본질적인'이라는 뜻인데, 프로그래밍에서는 주로 내장함수를 의미한다고 한다. 그래서 구현은 볼 수 없고, 그냥 문서 읽으면서 가져다쓰면 되는 것 같다.

FORCEINLINE float InvSqrt(float InValue)
{
    const __m128 One = _mm_set_ss(1.0f);
    const __m128 Y0 = _mm_set_ss(InValue);
    const __m128 X0 = _mm_sqrt_ss(Y0);
    const __m128 R0 = _mm_div_ss(One, X0);
    float temp;
    _mm_store_ss(&temp, R0);
    return temp;
}

오케이, 그럼 _mm으로 시작하는 함수들도 그냥 SSE를 사용할 수 있도록 만들어준 함수렷다. 대충 코드의 흐름을 보아하니 파라미터로 들어온 값에 루트 씌우고 역수를 구하는 간단한 코드다. 흔히 말하는 고속 역제곱근 코드는 사용하지 않고, SIMD를 사용하여 정직하게 연산한다.

그러면 _mm_set_ss는 뭘까? 개발자 문서를 보니 그냥 movss 명령이라고 한다.

실제로 (Release 옵션으로) 디스어셈블 해보면 movss 명령을 수행한다.

그런데, 마지막 의문이 하나 있다. 왜 rsqrt를 사용하지 않고 직접 역수를 구하는 걸까. 해답을 찾기 위해 인텔 개발자 문서를 찾아보니 rsqrt는 값을 근사(approximate)하는 명령이라고 한다. 오차는 최대 1.5*2^-12인데, 반올림해서 대충 0.0004 정도 된다. 이 정도면 오차가 충분히 작지 않나 싶은데, 에픽게임즈의 판단은 아니었나보다.

 

대신, GetInvSqrtEst 함수를 통해 rsqrt를 사용한 근사값을 구하는 함수가 구현되어있다. 물론 뉴턴-랩슨 이터레이션 한 번을 거치긴 하는데... 일단 설명을 이어나가보겠다. 

언리얼 엔진의 GetInvSqrtEst 함수 분석

FORCEINLINE float InvSqrtEst(float F)
{
    // Performs one pass of Newton-Raphson iteration on the hardware estimate
    const __m128 fOneHalf = _mm_set_ss(0.5f);
    __m128 Y0, X0, X1, FOver2;
    float temp;

    Y0 = _mm_set_ss(F);
    X0 = _mm_rsqrt_ss(Y0);	// 1/sqrt estimate (12 bits)
    FOver2 = _mm_mul_ss(Y0, fOneHalf);

    // 1st Newton-Raphson iteration
    X1 = _mm_mul_ss(X0, X0);
    X1 = _mm_sub_ss(fOneHalf, _mm_mul_ss(FOver2, X1));
    X1 = _mm_add_ss(X0, _mm_mul_ss(X0, X1));

    _mm_store_ss(&temp, X1);
    return temp;
}

 

Est는 대충 Estimate 같은 약자일테니 역제곱근을 근사해서 구하는 함수로 이해할 수 있겠다. 특이한 점은, 뉴턴-랩슨 이터레이션을 한 번 거쳐서 오차를 보정한다.

 

$$x_{x+1}=x_n-{{f(x_n)}\over{f'(x_n)}}​$$

일단 뉴턴-랩슨법은 위 공식에 따라 비선형 방정식의 해를 근사하는 방법이다.

 

그리고 우리는 $1\over\sqrt{F}$을 구하는게 목표이다. 이 값을 $x$라고 했을 때, $x$를 해로 갖는 비선형 방정식을 떠올리면 아래와 같은 식을 얻을 수 있다.

$$f(x)={{1}\over{x^2}}-F$$

그러면 도함수는 아래와 같다.

$$f'(x)=-{{2}\over{x^3}}$$

 

한편, 뉴턴-랩슨법을 통해 해를 구하기 위해서는 초기값이 필요한데, rsqrt 명령을 통해서 초기값을 구했다. 이 값을 $x_0$이라고 하자. 그러면 $x_1$을 다음과 같이 구해 보정할 수 있다. 식이 지저분해서 정리하는 과정은 생략한다.

 

$$x_{1} = x_0 + \frac{x_0 \left(1 - F x_0^2\right)}{2}$$

자, 그러면 코드에서 X1을 구하는 과정이 위 수식을 그대로 옮긴 것임을 알 수 있다.

 

이제 내 렌더러에서 역제곱근을 구하는 코드를 손 보자.

GetInvSqrt 함수 수정

struct Math
{
    // ...
    static float GetInvSqrt(const float inValue)
    {
        if (MachineInfo::GetInstance()->IsSseSupport())
        {
            const __m128 one = _mm_set_ss(1.0f);
            const __m128 val = _mm_set_ss(inValue);
            const __m128 sqrtVal = _mm_sqrt_ss(val);
            const __m128 res = _mm_div_ss(one, sqrtVal);
            float ret;
            _mm_store_ss(&ret, res);
            return ret;
        }

        constexpr uint8 newtonRaphsonIteration = 3;

        const float x2 = inValue * 0.5f;
        float y = inValue;
        int i = *std::bit_cast<int*>(&y);
        i = 0x5f3759df - (i >> 1);
        y = *std::bit_cast<float*>(&i);

        for (uint8 iter = 0; iter < newtonRaphsonIteration; ++iter)
        {
            constexpr float threeHalfs = 1.5f;
            y = y * (threeHalfs - (x2 * y * y));
        }

        return y;
    }
    // ...   
}

그러면 뭐, 요 정도로 수정해보고자 한다. 근사값을 구하는 함수를 구분하지는 않았고, SSE를 지원하는지 체크한 다음 SSE를 사용할지, 고속역제곱근 알고리즘을 사용할지 결정하는 구조이다.

MachineInfo::MachineInfo()
{
	int cpuInfo[4];
	__cpuid(cpuInfo, 1);
	mbIsSseSupport = (cpuInfo[3] & (1 << 25)) != 0;
}

MachineInfo* MachineInfo::GetInstance()
{
	static MachineInfo sInstance;
	return &sInstance;
}

MachineInfo 클래스는 싱글톤이고, __cpuid를 통해서 SSE 지원 여부를 체크해준다(아직은 이 기능밖에 없다). 해당 코드는 구글링해서 찾아온 코드인데, 제대로 돌지 의문스러워서 이리저리 찾아보았다.

일단 MSDN을 보면 입력으로 받은 정수 배열은 EAX, EBX, ECX, EDX의 정보를 담아줄 배열이다. 그리고 function_id에 어떤 함수를 호출할 지 적으면 된다. MS-DOS에서 21번 인터럽트를 발생시켜서 핸들러를 사용하는 것과 유사해보인다.

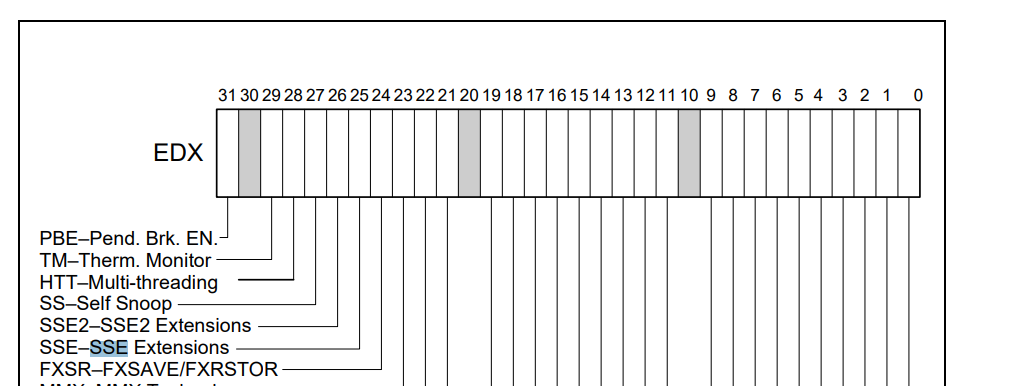
그리고 인텔과 AMD 모두 EDX의 25번째 비트를 통해 SSE 지원여부를 반환한다는 것을 확인했다(혹시나 둘이 다를까봐 긴장했음).

mbIsSseSupport = (cpuInfo[3] & (1 << 25)) != 0;

그래서 SSE 지원 여부는 요렇게 EDX에서 비트25를 마스킹해서 확인할 수 있다.

마치며

사실 벡터 연산이 아니라서 SIMD가 큰 의미가 있는지는 모르겠지만... 일단 언리얼 엔진에서 봤던 코드를 이해하고 써먹어봤다는 일종의 자기만족 정도로 넘어갈 생각이다.